Power System Analysis
High Voltage Dc Transmission
Marks 11
GATE EE 2011
MCQ (Single Correct Answer)
+2
-0.6
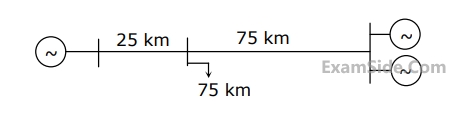
A load center of 120 MW derives power from two power stations connected by 220 kV transmission lines of 25 km and 75 km as shown in the figure below. The three generators G1,G2 and G3 are of 100 MW capacity each and have identical fuel cost characteristics. The minimum loss generation schedule for supplying the 120 MW load is

2
GATE EE 2009
MCQ (Single Correct Answer)
+2
-0.6
Three generators are feeding a load of $$100$$ $$MW$$. The details of the generators Rating, Efficiency and Regulation are shown below


In the event of increased load power demand, which of the following will happen?
3
GATE EE 2008
MCQ (Single Correct Answer)
+2
-0.6
A lossless power system has to serve a load of $$250$$ $$MW.$$ There are two generators ($$G1$$ and $$G2$$) in the system with cost curves $${C_1}$$ and $${C_2}$$ respectively defined as follows:
$${C_1}\left( {{P_{G1}}} \right) = {P_{G1}} + 0.055 \times P_{G1}^2$$
$${C_2}\left( {{P_{G2}}} \right) = 3{P_{G2}} + 0.03 \times P_{G2}^2$$
Where $${P_{G1}}$$ and $${P_{G2}}$$ are the MW injections from generator $${G_1}$$ and $${G_2}$$ respectively. Thus, the minimum cost dispatch will be
$${C_1}\left( {{P_{G1}}} \right) = {P_{G1}} + 0.055 \times P_{G1}^2$$
$${C_2}\left( {{P_{G2}}} \right) = 3{P_{G2}} + 0.03 \times P_{G2}^2$$
Where $${P_{G1}}$$ and $${P_{G2}}$$ are the MW injections from generator $${G_1}$$ and $${G_2}$$ respectively. Thus, the minimum cost dispatch will be
4
GATE EE 2005
MCQ (Single Correct Answer)
+2
-0.6
A load centre is at an equidistant from the two thermal generating stations $${G_1}$$ and $${G_2}$$ as shown in figure. The fuel cost characteristics of the generating stations are given by
$${F_1} = a + b{P_1} + cP_1^2\,Rs/hour$$
$${F_2} = a + b{P_2} + 2cP_2^2\,Rs/hour$$
$${F_1} = a + b{P_1} + cP_1^2\,Rs/hour$$
$${F_2} = a + b{P_2} + 2cP_2^2\,Rs/hour$$

Where $${P_1}$$ and $${P_2}$$ are the generations in $$MW$$ of $${G_1}$$and $${G_2}$$, respectively. For most economic generation to meet $$300MW$$ of load $${P_1}$$ and $${P_2},$$ respectively, are
GATE EE Subjects
Electromagnetic Fields
Signals and Systems
Engineering Mathematics
General Aptitude
Power Electronics
Power System Analysis
Analog Electronics
Control Systems
Digital Electronics
Electrical Machines
Electric Circuits
Electrical and Electronics Measurement