Signals and Systems
Miscellaneous
Marks 21
GATE EE 2014 Set 3
MCQ (Single Correct Answer)
+1
-0.3
A function f(t) is shown in the figure.
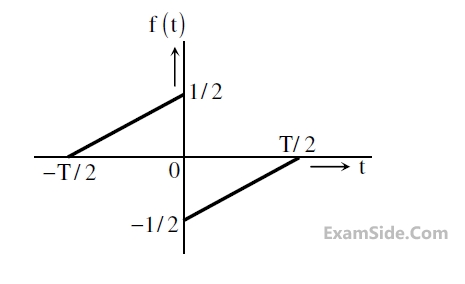 The Fourier transform F($$\mathrm\omega$$) of f(t) is
The Fourier transform F($$\mathrm\omega$$) of f(t) is
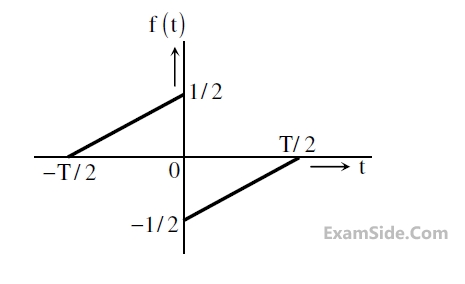 The Fourier transform F($$\mathrm\omega$$) of f(t) is
The Fourier transform F($$\mathrm\omega$$) of f(t) is
2
GATE EE 2014 Set 3
MCQ (Single Correct Answer)
+1
-0.3
A signal is represented by $$$x\left(t\right)=\left\{\begin{array}{l}1\;\;\;\left|t\right|\;<\;1\\0\;\;\;\left|t\right|\;>\;1\end{array}\right.$$$
The Fourier transform of the convolved signal y(t)=x(2t) * x(t/2) is
Questions Asked from Marks 1
GATE EE Subjects
Electromagnetic Fields
Signals and Systems
Engineering Mathematics
General Aptitude
Power Electronics
Power System Analysis
Analog Electronics
Control Systems
Digital Electronics
Electrical Machines
Electric Circuits
Electrical and Electronics Measurement