Signals and Systems
1
GATE ECE 2002
Subjective
+5
-0
A deterministic signal x(t) = $$\cos (2\pi t)$$ is passed through a differentiator as shown in
Figure.

(a) Determine the autocorrelation Rxx ($$\tau $$) and the power spectral density Sxx(f).
(b) Find the output power spectral density Syy( f ).
(c) Evaluate Rxy(0) and Rxy(1/4).

(a) Determine the autocorrelation Rxx ($$\tau $$) and the power spectral density Sxx(f).
(b) Find the output power spectral density Syy( f ).
(c) Evaluate Rxy(0) and Rxy(1/4).
2
GATE ECE 2000
Subjective
+5
-0
For the linear, time-invariant system whose block diagram is shown in Fig.(a),
with input x(t) and output y(t).
(a) Find the transfer function.
(b) For the step response of the system [i.e. find y(t) when x(t) is a unit step function and the initial conditions are zero]
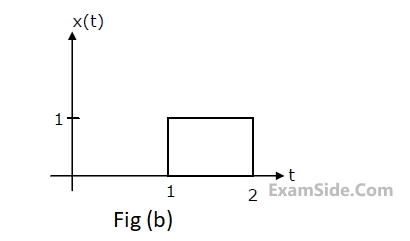
(c) Find y(t), if x(t) is as shown in Fig.(b), and the initial conditions are zero.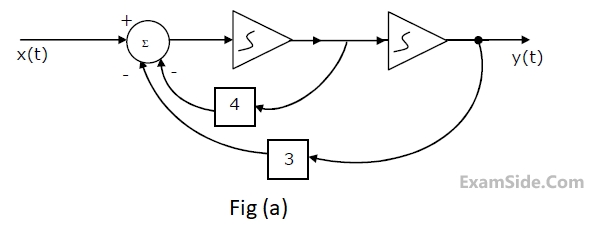
(a) Find the transfer function.
(b) For the step response of the system [i.e. find y(t) when x(t) is a unit step function and the initial conditions are zero]
(c) Find y(t), if x(t) is as shown in Fig.(b), and the initial conditions are zero.


3
GATE ECE 1997
Subjective
+5
-0
Fig.1, shows the block diagram representation of a control system. The system in block A has an impulse response $${h_A}(t) = {e^{ - t}}\,u(t)$$. The system in block B has an impulse response $${h_B}(t) = {e^{ - 2t}}\,u(t)$$. The block 'k' amplifies its input by a factor k. For the overall system with input x(t) and output y(t)
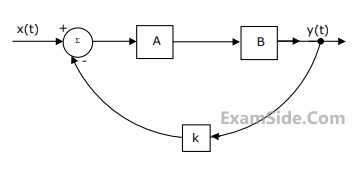

(a) Find the transfer function $${{Y(s)} \over {X(s)}}$$, when k=1
(b) Find the impulse response, when k = 0
(c) Find the value of k for which the system becomes unstable.
$$$\left[ {\matrix{ {Note:u(t)\, \equiv \,0} & {t\, \le \,0} \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \equiv 1} & {t\, > \,0} \cr } } \right]$$$
4
GATE ECE 1993
Subjective
+5
-0
Consider the following interconnection of the three LTI systems (Fig.1). $${h_1}(t)$$ , $${h_2}(t)$$ and $${h_3}(t)$$ are the impulse responses of these three LTI systems with $${H_1}(\omega )$$, $${H_2}(\omega )$$, and $${H_3}(\omega )$$ as their respective Fourier transforms. Given that $${h_1}\,(t)\, = \,{d \over {dt}}\left[ {{{\sin ({\omega _0}t)} \over {2\,\pi \,t}}} \right],{H_2}(\omega ) = \exp \left( {{{ - j2\pi \omega } \over {{\omega _0}}}} \right)$$
$${h_3}\,(t)\, = u(t)\,and\,x(t)\, = \,\sin \,2\,{\omega _0}t\, + \,\cos \,({\omega _0}t/2),$$ find the output y(t).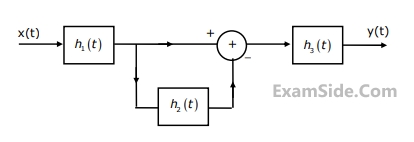
$${h_3}\,(t)\, = u(t)\,and\,x(t)\, = \,\sin \,2\,{\omega _0}t\, + \,\cos \,({\omega _0}t/2),$$ find the output y(t).

Questions Asked from Marks 5
GATE ECE Subjects
Signals and Systems
Network Theory
Control Systems
Digital Circuits
General Aptitude
Electronic Devices and VLSI
Analog Circuits
Engineering Mathematics
Microprocessors
Communications
Electromagnetics