Control Systems
1
GATE ECE 2007
MCQ (Single Correct Answer)
+2
-0.6
A control system with a PD controller is shown in the figure. If the velocity error constant $${K_v} = 1000$$ and the damping ratio $$\zeta = 0.5,$$ then the values of $${K_P}$$ and $${K_D}$$ are
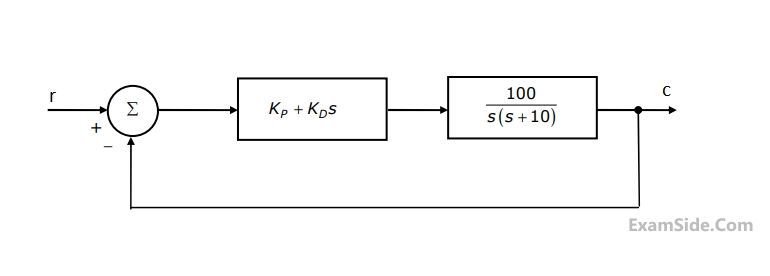

2
GATE ECE 2007
MCQ (Single Correct Answer)
+2
-0.6
The open-loop transfer function of a plant is given as $$G(s) = {1 \over {{s^2} - 1}}.$$ If the plant is operated in a unity feedback configuration, then the lead compensator that can stabilize this control system is
3
GATE ECE 2005
MCQ (Single Correct Answer)
+2
-0.6
A double integrator plant, $$G(s) = {K \over {{s^2}}},H(s) = 1$$ is to be compensated to achieve the damping ratio $$\zeta = 0.5$$ and an undamped natural frequency, $${\omega _n} = 5$$ rad/sec. Which one of the following compensator $${G_c}(s)$$ will be suitable?
4
GATE ECE 1992
MCQ (Single Correct Answer)
+2
-0.6
A process with open-loop model
$$G(s) = {{K{e^{ - s{\tau _d}}}} \over {\tau s + 1}},$$ is controlled by a PID controller. For this process
GATE ECE Subjects
Signals and Systems
Network Theory
Control Systems
Digital Circuits
General Aptitude
Electronic Devices and VLSI
Analog Circuits
Engineering Mathematics
Microprocessors
Communications
Electromagnetics