Control Systems
1
GATE ECE 2000
Subjective
+5
-0
A certain linear, time-invariant system has the state and output representation shown below:
$$$\eqalign{
& \left[ {\matrix{
{\mathop {{x_1}}\limits^ \bullet } \cr
{\mathop {{x_2}}\limits^ \bullet } \cr
} } \right] = \left[ {\matrix{
{ - 2} & 1 \cr
0 & { - 3} \cr
} } \right]\left[ {\matrix{
{{x_1}} \cr
{{x_2}} \cr
} } \right] + \left[ {\matrix{
1 \cr
0 \cr
} } \right]u \cr
& y = \left( {\matrix{
1 & 1 \cr
} } \right)\left[ {\matrix{
{{x_1}} \cr
{{x_2}} \cr
} } \right] \cr} $$$
(a) Find the eigen values (natural frequencies) of the system.
(b)If u(t)=$$\delta \left( t \right)$$ and x1(0+)=x2(0+)=0, find x1(t),x2(t) and y(t), for t>0.
(c)When the input is zero, choose initial conditions $${x_1}\left( {{0^ + }} \right)$$ and $${x_2}\left( {{0^ + }} \right)$$ such that $$y\left( t \right) = A{e^{ - 2t}}$$ for t>0
(a) Find the eigen values (natural frequencies) of the system.
(b)If u(t)=$$\delta \left( t \right)$$ and x1(0+)=x2(0+)=0, find x1(t),x2(t) and y(t), for t>0.
(c)When the input is zero, choose initial conditions $${x_1}\left( {{0^ + }} \right)$$ and $${x_2}\left( {{0^ + }} \right)$$ such that $$y\left( t \right) = A{e^{ - 2t}}$$ for t>0
2
GATE ECE 1997
Subjective
+5
-0
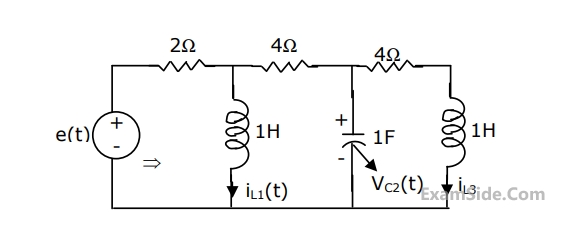
For the circuit shown in the figure, choose state variables as $${x_{1,}}{x_{2,}}{x_3}$$ to be $${i_{L1}}\left( t \right),{v_{c2}}\left( t \right),{i_{L3}}\left( t \right)$$
Wriote the state equations
$$$\left[ {\matrix{ {\mathop {{x_1}}\limits^ \bullet } \cr {\mathop {{x_2}}\limits^ \bullet } \cr {\mathop {{x_3}}\limits^ \bullet } \cr } } \right] = A\left[ {\matrix{ {{x_1}} \cr {{x_2}} \cr {{x_3}} \cr } } \right] + B\left[ {e\left( t \right)} \right]$$$3
GATE ECE 1996
Subjective
+5
-0
Obtain a state space representation in diagonal form for the following system
$$${{{d^3}y} \over {d{t^3}}} + 6{{{d^2}y} \over {d{t^2}}} + 11{{dy} \over {dt}} + 6y = 6u\left( t \right)$$$
Questions Asked from Marks 5
GATE ECE Subjects
Signals and Systems
Network Theory
Control Systems
Digital Circuits
General Aptitude
Electronic Devices and VLSI
Analog Circuits
Engineering Mathematics
Microprocessors
Communications
Electromagnetics