For a complex number $$z,$$
$$\mathop {Lim}\limits_{z \to i} {{{z^2} + 1} \over {{z^3} + 2z - i\left( {{z^2} + 2} \right)}}$$ is

Consider the function $$f\left( z \right) = z + {z^ * }$$ where $$z$$ is a complex variable and $${z^ * }$$ denotes its complex conjugate. Which one of the following is TRUE?

Given $$f\left( z \right) = g\left( z \right) + h\left( z \right),$$ where $$f,g,h$$ are complex valued functions of a complex variable $$z.$$ Which ONE of the following statements is TRUE?

All the values of the multi valued complex function $${1^i},$$ where $$i = \sqrt { - 1} $$ are

Integration of the complex function $$f\left( z \right) = {{{z^2}} \over {{z^2} - 1}},$$ in the counterclockwise direction, around $$\left| {z - 1} \right| = 1,$$ is

Square roots of $$-i,$$ where $$i = \sqrt { - 1} $$ are

Given $$X(z) = {z \over {{{(z - a)}^2}}}$$ with |z| > a, the residue of $$X(z){z^{n - 1}}$$ at z = a for $$n \ge 0$$ will be

Let $C$ be a clockwise oriented closed curve in the complex plane defined by $|\lambda|=1$. Further, let $f(x)=j z$ be a complex function, where $j=\sqrt{-1}$. Then, $\oint_C f(z) d z=$ ___________ .

The value of the contour integral in the complex - plane $$\oint {{{{z^3} - 2z + 3} \over {z - 2}}} dz$$ along the contour $$\left| z \right| = 3,$$ taken counter-clockwise is

Consider the line integral $${\rm I} = \int\limits_c {\left( {{x^2} + i{y^2}} \right)dz,} $$ where $$z=x+iy.$$ The line $$c$$ is shown in the figure below.

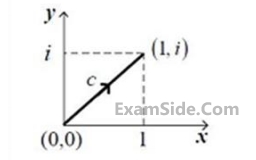
The value of $${\rm I}$$ is

The value of the integral $$\oint\limits_c {{{2z + 5} \over {\left( {z - {1 \over 2}} \right)\left( {{z^2} - 4z + 5} \right)}}} dz$$ over the contour $$\left| z \right| = 1,$$ taken in the anti-clockwise direction, would be

Let $$S$$ be the set of points in the complex plane corresponding to the unit circle. $$\left( {i.e.,\,\,S = \left\{ {z:\left| z \right| = 1} \right\}} \right.$$ Consider the function $$f\left( z \right) = z{z^ * }$$ where $${z^ * }$$ denotes the complex conjugate of $$z.$$ The $$f(z)$$ maps $$S$$ to which one of the following in the complex plane?

$$\oint {{{{z^2} - 4} \over {{z^2} + 4}}} dz\,\,$$ evaluated anticlockwise around the circular $$\left| {z - i} \right| = 2,$$ where $$i = \sqrt { - 1} $$, is

Given $$f\left( z \right) = {1 \over {z + 1}} - {2 \over {z + 3}}.$$ If $$C$$ is a counterclockwise path in the $$z$$-plane such that
$$\left| {z + 1} \right| = 1,$$ the value of $${1 \over {2\,\pi \,j}}\oint\limits_c {f\left( z \right)dz} $$ is

If $$x = \sqrt { - 1} ,\,\,$$ then the value of $${X^x}$$ is

A point $$z$$ has been plotted in the complex plane as shown in the figure below

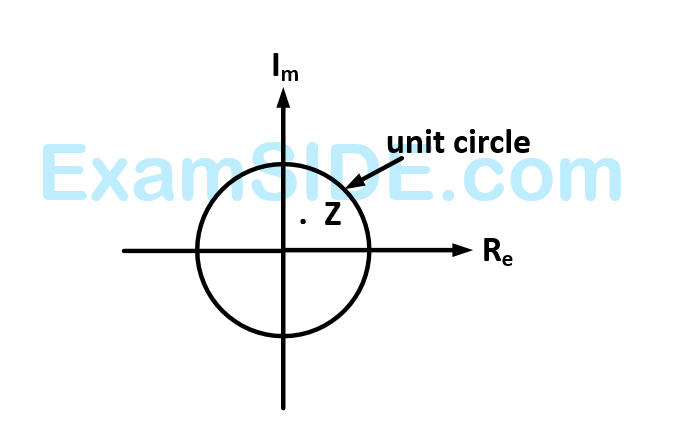
The plot of the complex number $$w = 1/z$$