Network Theory
State Equations For Networks
Marks 51
GATE ECE 2023
Numerical
+1
-0
For the two port network shown below, the [Y]-parameters is given as
$$[Y] = {1 \over {100}}\left[ {\matrix{ 2 & { - 1} \cr { - 1} & {4/3} \cr } } \right]S$$
The value of load impedance $$\mathrm{Z_L}$$, in $$\Omega$$, for maximum power transfer will be ___________ (rounded off to the nearest integer).

Your input ____
2
GATE ECE 2018
Numerical
+1
-0
The ABCD matrix for a two-port network is defined by :
$$\left[ {\matrix{ {{V_1}} \cr {{I_1}} \cr } } \right] = \left[ {\matrix{ A & B \cr C & D \cr } } \right]\left[ {\matrix{ {{V_2}} \cr { - {I_2}} \cr } } \right]$$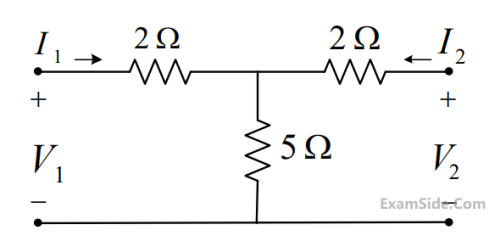
The parameter B for the given two-port network (in ohms, correct to two decimal places) is _______.
$$\left[ {\matrix{ {{V_1}} \cr {{I_1}} \cr } } \right] = \left[ {\matrix{ A & B \cr C & D \cr } } \right]\left[ {\matrix{ {{V_2}} \cr { - {I_2}} \cr } } \right]$$

The parameter B for the given two-port network (in ohms, correct to two decimal places) is _______.
Your input ____
3
GATE ECE 2016 Set 1
MCQ (Single Correct Answer)
+1
-0.3
Consider a two-port network with the transmission matrix: T = $$\begin{bmatrix}A&B\\C&D\end{bmatrix}$$. If the network is
reciprocal, then
4
GATE ECE 2016 Set 3
Numerical
+1
-0
The z-parameter matrix for the two-port network shown is $$$\left[ {\matrix{
{2\,j\,\omega } & {j\,\omega } \cr
{j\,\omega } & {3\, + \,2\,j\,\omega } \cr
} } \right]$$$
Where the entries are in $$\Omega $$. Suppose $$\,{Z_b}\,\left( {j\,\omega } \right) = {R_b} + j\,\omega $$
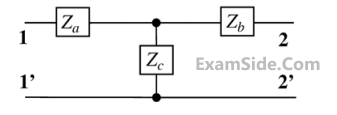 Then the value of $${R_b}$$ (in $$\Omega $$) equals _______________________3
Then the value of $${R_b}$$ (in $$\Omega $$) equals _______________________3
 Then the value of $${R_b}$$ (in $$\Omega $$) equals _______________________3
Then the value of $${R_b}$$ (in $$\Omega $$) equals _______________________3Your input ____
GATE ECE Subjects
Signals and Systems
Network Theory
Control Systems
Digital Circuits
General Aptitude
Electronic Devices and VLSI
Analog Circuits
Engineering Mathematics
Microprocessors
Communications
Electromagnetics