ExamSIDE
Questions (Powered by ExamGOAL)
Engineering Mathematics
Linear AlgebraCalculusVector CalculusComplex VariableProbability and StatisticsDifferential EquationsNumerical MethodsTransform Theory
Calculus
Practice Questions
Marks 1
1

Consider the following series:

(i) $\sum\limits_{n=1}^{\infty} \frac{1}{\sqrt{n}}$

(ii) $ \sum\limits_{n=1}^{\infty} \frac{1}{n(n+1)}$

(iii) $\sum\limits_{n=1}^{\infty} \frac{1}{n!}$

GATE ECE 2025
2

Consider the function $f: \mathbb{R} \rightarrow \mathbb{R}$ defined as

$$ f(x)=2 x^3-3 x^2-12 x+1 $$

Which of the following statements is/are correct?

(Here, $\mathbb{R}$ is the set of real numbers.)

GATE ECE 2025
3

Consider the two-dimensional vector field $$\overrightarrow F (x,y) - x\overrightarrow i + y\overrightarrow j $$, where $$\overrightarrow i $$ and $$\widehat j$$ denote the unit vectors along the x-axis and the y-axis, respectively. A contour C in the x-y plane, as shown in the figure, is composed of two horizontal lines connected at the two ends by two semicircular arcs of unit radius. The contour is traversed in the counter-clockwise sense. The value of the closed path integral

$$\oint\limits_C {\overrightarrow F (x,y)\,.\,(dx\overrightarrow i + dy\overrightarrow j )} $$

is ___________.

GATE ECE 2022 Engineering Mathematics - Calculus Question 8 English

GATE ECE 2022
4
The families of curves represented by the solution of the equation

$${{dy} \over {dx}} = - {\left( {{x \over y}} \right)^n}$$

for n = –1 and n = 1 respectively, are
GATE ECE 2019
5
Let $$f\left( {x,y} \right) = {{a{x^2} + b{y^2}} \over {xy}}$$, where $$a$$ and $$b$$ are constants. If $${{\partial f} \over {\partial x}} = {{\partial f} \over {\partial y}}$$ at x = 1 and y = 2, then the relation between $$a$$ and $$b$$ is
GATE ECE 2018
6
Taylor series expansion of $$f\left( x \right) = \int\limits_0^x {{e^{ - \left( {{{{t^2}} \over 2}} \right)}}} dt$$ around 𝑥 = 0 has the form

f(x) = $${a_0} + {a_1}x + {a_2}{x^2} + ...$$

The coefficient $${a_2}$$ (correct to two decimal places) is equal to _______.
GATE ECE 2018
7
The integral $$\int\limits_0^1 {{{dx} \over {\sqrt {\left( {1 - x} \right)} }}} $$ is equal ________.
GATE ECE 2016 Set 3
8
As $$x$$ varies from $$- 1$$ to $$3,$$ which of the following describes the behavior of the function $$f\left( x \right) = {x^3} - 3{x^2} + 1?$$
GATE ECE 2016 Set 2
9
How many distinct values of $$x$$ satisfy the equation $$sin(x)=x/2,$$ where $$x$$ is in radians ?
GATE ECE 2016 Set 2
10
Given the following statements about a function $$f:R \to R,$$ select the right option:
$$P:$$ If $$f(x)$$ is continuous at $$x = {x_0},$$ then it is also differentiable at $$x = {x_0},$$
$$Q:$$ If $$f(x)$$ is continuous at $$x = {x_0},$$ then it may not be differentiable at $$x = {x_0},$$
$$R:$$ If $$f(x)$$ is differentiable at $$x = {x_0},$$ then it is also continuous at $$x = {x_0},$$
GATE ECE 2016 Set 1
11
The contour on the $$x-y$$ plane, where the partial derivative of $${x^2} + {y^2}$$ with respect to $$y$$ is equal to the partial derivative of $$6y+4x$$ with respect to $$'x',$$ is
GATE ECE 2015 Set 3
12
The value of $$\sum\limits_{n = 0}^\infty {n{{\left( {{1 \over 2}} \right)}^n}\,\,} $$ is _______.
GATE ECE 2015 Set 3
13
A function $$f\left( x \right) = 1 - {x^2} + {x^3}\,\,$$ is defined in the closed interval $$\left[ { - 1,1} \right].$$ The value of $$x,$$ in the open interval $$(-1,1)$$ for which the mean value theorem is satisfied, is
GATE ECE 2015 Set 1
14
The series $$\sum\limits_{n = 0}^\infty {{1 \over {n!}}\,} $$ converges to
GATE ECE 2014 Set 4
15
The maximum value of the function $$\,f\left( x \right) = \ln \left( {1 + x} \right) - x$$ (where $$x > - 1$$ ) occurs at $$x=$$________.
GATE ECE 2014 Set 3
16
If $$z=xy$$ $$ln(xy),$$ then
GATE ECE 2014 Set 3
17
For $$0 \le t < \infty ,$$ the maximum value of the function $$f\left( t \right) = {e^{ - t}} - 2{e^{ - 2t}}\,$$ occurs at
GATE ECE 2014 Set 2
18
The value of $$\mathop {\lim }\limits_{x \to \infty } {\left( {1 + {1 \over x}} \right)^x}\,\,$$ is
GATE ECE 2014 Set 2
19
If $$\,{e^y} = {x^{1/x}}\,\,$$ then $$y$$ has a
GATE ECE 2010
20
For real values of $$x,$$ the minimum value of function $$f\left( x \right) = {e^x} + {e^{ - x}}\,\,$$ is
GATE ECE 2008
21
Which of the following function would have only odd powers of $$x$$ in its Taylor series expansion about the point $$x=0$$ ?
GATE ECE 2008
22
$$\mathop {Lim}\limits_{\theta \to 0} {{\sin \left( {\theta /2} \right)} \over \theta }\,\,\,$$ is
GATE ECE 2007
23
The following plot shows a function $$y$$ which varies linearly with $$x$$. The value of the integral $$\,\,{\rm I} = \int\limits_1^2 {y\,dx\,\,} $$ GATE ECE 2007 Engineering Mathematics - Calculus Question 49 English
GATE ECE 2007
24
For the function $${e^{ - x}},$$ the linear approximation around $$x=2$$ is
GATE ECE 2007
25
For $$\left| x \right| < < 1,\,\cot \,h\left( x \right)\,\,\,$$ can be approximated as
GATE ECE 2007
26
The value of the integral $$1 = {1 \over {\sqrt {2\pi } }}\,\,\int\limits_0^\infty {{e^{ - {\raise0.5ex\hbox{$\scriptstyle {{x^2}}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 8$}}}}} \,\,dx\,\,\,$$ is ________.
GATE ECE 2005
27
The curve given by the equation $${x^2} + {y^2} = 3axy$$ is
GATE ECE 1997
28
By reversing the order of integration $$\int\limits_0^2 {\int\limits_{{x^2}}^{2x} {f\left( {x,y} \right)dy\,dx} } $$ may be represented as ______.
GATE ECE 1995
29
The third term in the taylor's series expansion of $${e^x}$$ about $$'a'$$ would be ________.
GATE ECE 1995
30
The function $$y = {x^2} + {{250} \over x}$$ at $$x=5$$ attains
GATE ECE 1994
Marks 2
1

Consider a non-negative function $f(x)$ which is continuous and bounded over the interval $[2,8]$. Let $M$ and $m$ denote, respectively, the maximum and the minimum values of $f(x)$ over the interval.

Among the combinations of $\alpha$ and $\beta$ given below, choose the one(s) for which the inequality

$$ \beta \leq \int_2^8 f(x) d x \leq \alpha $$

is guaranteed to hold.

GATE ECE 2025
2

Consider the Earth to be a perfect sphere of radius $R$. Then the surface area of the region, enclosed by the 60°N latitude circle, that contains the north pole in its interior is _______.

GATE ECE 2024
3

The value of the line integral $$\int_P^Q {({z^2}dx + 3{y^2}dy + 2xz\,dz)} $$ along the straight line joining the points $$P(1,1,2)$$ and $$Q(2,3,1)$$ is

GATE ECE 2023
4

The value of the integral $$\int\limits\!\!\!\int_R {xy\,dx\,dy} $$ over the regioin R, given in the figure, is _________ (rounded off to the nearest integer).

GATE ECE 2023 Engineering Mathematics - Calculus Question 6 English

GATE ECE 2023
5

The function f(x) = 8loge x $$-$$ x2 + 3 attains its minimum over the interval [1, e] at x = __________.

(Here loge x is the natural logarithm of x.)

GATE ECE 2022
6

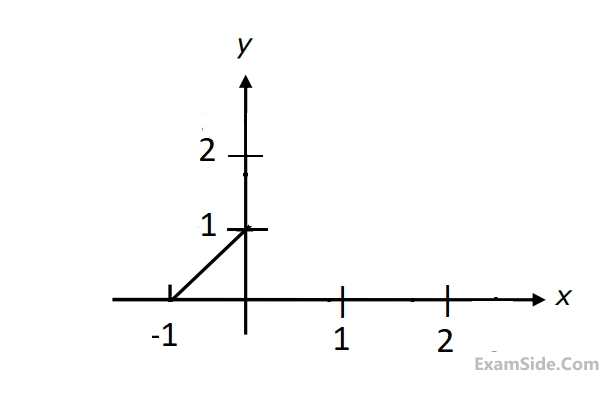
The value of the integral

$$\int\!\!\!\int\limits_D {3({x^2} + {y^2})dx\,dy} $$,

where D is the shaded triangular region shown in the diagram, is ___________ (rounded off to the nearest integer).

GATE ECE 2022 Engineering Mathematics - Calculus Question 9 English

GATE ECE 2022
7
Let r = x2 + y - z and z3 - xy + yz + y3 = 1. Assume that x and y are independent variables. At (x, y, z) = (2, -1, 1), the value (correct to two decimal places) of $${{\partial r} \over {\partial x}}$$ is ________________.
GATE ECE 2018
8
The minimum value of the function $$f\left( x \right) = {1 \over 3}x\left( {{x^2} - 3} \right)\,\,$$ in the interval $$ - 100 \le x \le $$ $$100$$ occurs at $$x=$$ __________.
GATE ECE 2017 Set 2
9
The values of the integrals $$\int\limits_0^1 {\left( {\int\limits_0^1 {{{x - y} \over {{{\left( {x + y} \right)}^3}}}dy} } \right)} dx\,\,$$ and $$\,\,\int\limits_0^1 {\left( {\int\limits_0^1 {{{x - y} \over {{{\left( {x + y} \right)}^3}}}dx} } \right)} dy\,\,$$ are
GATE ECE 2017 Set 2
10
A three dimensional region $$R$$ of finite volume is described by $$\,\,{x^2} + {y^2} \le {z^3},\,\,\,0 \le z \le 1$$
Where $$x, y, z$$ are real. The volume of $$R$$ correct to two decimal places is __________.
GATE ECE 2017 Set 1
11
Let $$\,\,f\left( x \right) = {e^{x + {x^2}}}\,\,$$ for real $$x.$$ From among the following. Choose the Taylor series approximation of $$f$$ $$(x)$$ around $$x=0,$$ which includes all powers of $$x$$ less than or equal to $$3.$$
GATE ECE 2017 Set 1
12
A triangle in the $$xy-$$plane is bounded by the straight lines $$2x=3y, y=0$$ and $$x=3.$$ The volume above the triangle and under the plane $$x+y+z=6Z$$ is ________.
GATE ECE 2016 Set 3
13
The integral $$\,\,{1 \over {2\pi }}\int {\int_D {\left( {x + y + 10} \right)dxdy\,\,} } $$ where $$D$$ denotes the disc: $${x^2} + {y^2} \le 4,$$ evaluates to _________.
GATE ECE 2016 Set 1
14
The region specified by
$$\left\{ {\left( {\rho ,\varphi ,{\rm Z}} \right):3 \le \rho \le 5,\,\,{\pi \over 8} \le \phi \le {\pi \over 4},\,\,3 \le z \le 4.5} \right\}$$ in cylindrical coordinates has volume of ___________.
GATE ECE 2016 Set 1
15
The value of the integral $$\int_{ - \infty }^\infty {12\,\,\cos \left( {2\pi t} \right){{\sin \left( {4\pi t} \right)} \over {4\pi t}}} dt\,\,$$ is __________.
GATE ECE 2015 Set 2
16
Which one of the following graphs describes the function? $$f\left( x \right) = {e^{ - x}}\left( {{x^2} + x + 1} \right)\,?$$
GATE ECE 2015 Set 1
17
The maximum area (in square units) of a rectangle whose vertices lie on the ellipse $${x^2} + 4{y^2} = 1\,\,$$ is
GATE ECE 2015 Set 1
18
The Taylor series expansion of $$3$$ $$sin$$ $$x$$ $$+2cos$$ $$x$$ is
GATE ECE 2014 Set 1
19
The volume under the surface $$z\left( {x,y} \right) = x + y$$ and above the triangle in the $$xy$$ plane defined by $$\left\{ {0 \le y \le x} \right.$$ and $$\,\left. {0 \le x \le 12} \right\}$$ is _________.
GATE ECE 2014 Set 1
20
For a right angled triangle, if the sum of the lengths of the hypotenuse and a side is kept constant, in order to have maximum area of the triangle, the angle between the hypotenuse and the side is
GATE ECE 2014 Set 4
21
The maximum value of $$f\left( x \right) = 2{x^3} - 9{x^2} + 12x - 3$$
in the interval $$\,0 \le x \le 3$$ is __________.
GATE ECE 2014 Set 3
22
The Taylor series expansion of $$\,\,{{\sin x} \over {x - \pi }}\,\,$$ at $$x = \pi $$ is given by
GATE ECE 2009
23
The value of the integral of the function $$\,\,g\left( {x,y} \right) = 4{x^3} + 10{y^4}\,\,$$ along the straight line segment from the point $$(0,0)$$ to the point $$(1,2)$$ in the $$xy$$ -plane is
GATE ECE 2008
24
In the Taylor series expansion of $${e^x} + \sin x$$ about the point $$x = \pi ,$$ the coefficient of $${\left( {x = \pi } \right)^2}$$ is
GATE ECE 2008
25
Consider the function $$\,f\left( x \right) = {x^2} - x - 2.\,$$ The maximum value of $$f(x)$$ in the closed interval $$\left[ { - 4,4} \right]\,$$
GATE ECE 2007
26
$$\int\limits_0^{{\raise0.5ex\hbox{$\scriptstyle \pi $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}} {\int\limits_0^{{\raise0.5ex\hbox{$\scriptstyle \pi $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}} {\sin \left( {x + y} \right)dx\,dy} } $$
GATE ECE 2000