
A waveguide consists of two infinite parallel plates (perfect conductors) at a separation of 10$$-$$4 cm, with air as the dielectric. Assume the speed of light in air to be 3 $$\times$$ 108 m/s. The frequency/frequencies of TM waves which can propagate in this waveguide is/are ___________.
The cross-sectional dimemsions of the waveguide are given as a = 0.08 m and b = 0.033 m. The mode of propagation inside the waveguide is
$$\cos \,\,(6.283\,\, \times \,\,{10^{10}}t\, - \beta \,z)$$
The phase velocity $${V_p}$$ of the wave inside the waveguide satisfies

where $${H_0}$$ is a constant, a and b are the dimensions along the x-axis and the y-axis respectively. The mode of propagation in the waveguide is

For a wave propagating in an air filled rectangular wave guide
Where $$k = \,\,\eta \,\omega \,\, \in $$
(a) Determine the surface charge densities $${\rho _s}$$ on the plates at x = 0 and x = d
(b) Determine the surface current densities $$\mathop {{J_s}}\limits^ \to $$ on the same plates.
(c) Prove that $${\rho _s}$$ and $$\mathop {{J_s}}\limits^ \to $$ satisfy the current continuity condition.

Where $$k = \,\,\eta \,\omega \,\, \in $$
(a) Determine the surface charge densities $${\rho _s}$$ on the plates at x = 0 and x = d
(b) Determine the surface current densities $$\mathop {{J_s}}\limits^ \to $$ on the same plates.
(c) Prove that $${\rho _s}$$ and $$\mathop {{J_s}}\limits^ \to $$ satisfy the current continuity condition.

Where $$k = \,\,\eta \,\omega \,\, \in $$
(a) Determine the surface charge densities $${\rho _s}$$ on the plates at x = 0 and x = d
(b) Determine the surface current densities $$\mathop {{J_s}}\limits^ \to $$ on the same plates.
(c) Prove that $${\rho _s}$$ and $$\mathop {{J_s}}\limits^ \to $$ satisfy the current continuity condition.

(a) Calculate the cut-off wavelength and the guide wavelength for this mode.
(b) What are the other (TE or TM) modes that can propagate through the waveguide?
(c) If a = b = 2.29 cm, what are the modes which can propagate through the waveguide?
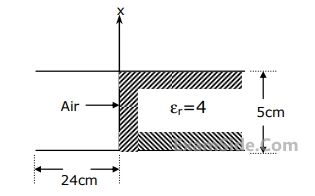
Find the vector magnetic field and the phase velocity of the wave inside the waveguide.
(i) Determine the cutoff frequency of the$$T{E_{11}}$$ mode.
(ii) Determine the frequency at which this / mode has an attenuation of $$3\,\pi $$ nepers/m.
(i) Determine the cutoff frequency of the$$T{E_{11}}$$ mode.
(ii) Determine the frequency at which this / mode has an attenuation of $$3\,\pi $$ nepers/m.