Consider an additive white Gaussian noise (AWGN) channel with bandwidth $W$ and noise power spectral density $\frac{N_o}{2}$. Let $P_{a v}$ denote the average transmit power constraint. Which one of the following plots illustrates the dependence of the channel capacity $C$ on the bandwidth $W$ (keeping $P_{a v}$ and $N_0$ fixed)?
The generator matrix of a $(6,3)$ binary linear block code is given by
$$ G=\left[\begin{array}{llllll} 1 & 0 & 0 & 1 & 0 & 1 \\ 0 & 1 & 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & 1 & 1 & 0 \end{array}\right] $$
The minimum Hamming distance $d_{\min }$ between codewords equals___________ (answer in integer).
A source transmits symbols from an alphabet of size 16. The value of maximum achievable entropy (in bits) is _______ .
The random variable $X$ takes values in $\{-1,0,1\}$ with probabilities $P(X=-1)=P(X=1)$ and $\alpha$ and $P(X=0)=1-2 \alpha$, where $0<\alpha<\frac{1}{2}$.
Let $g(\alpha)$ denote the entropy of $X$ (in bits), parameterized by $\alpha$. Which of the following statements is/are TRUE?
$X$ and $Y$ are Bernoulli random variables taking values in $\{0,1\}$. The joint probability mass function of the random variables is given by:
$$ \begin{aligned} & P(X=0, Y=0)=0.06 \\ & P(X=0, Y=1)=0.14 \\ & P(X=1, Y=0)=0.24 \\ & P(X=1, Y=1)=0.56 \end{aligned} $$
The mutual information $I(X ; Y)$ is ___________(rounded off to two decimal places).
The frequency of occurrence of 8 symbols (a-h) is shown in the table below. A symbol is chosen and it is determined by asking a series of "yes/no" questions which are assumed to be truthfully answered. The average number of questions when asked in the most efficient sequence, to determine the chosen symbol, is _____________ (rounded off to two decimal places).
| Symbols | a | b | c | d | e | f | g | h |
|---|---|---|---|---|---|---|---|---|
| Frequency of occurrence | $$\frac{1}{2}$$ | $${1 \over 4}$$ | $${1 \over 8}$$ | $${1 \over {16}}$$ | $${1 \over {32}}$$ | $${1 \over {64}}$$ | $${1 \over {128}}$$ | $${1 \over {128}}$$ |
The transition diagram of a discrete memoryless channel with three input symbols and three output symbols is shown in the figure. The transition probabilities are as marked. The parameter $$\alpha$$ lies in the interval [0.25, 1]. The value of .. for which the capacity of this channel is maximized, is __________ (rounded off to two decimal places).
Consider communication over a memoryless binary symmetric channel using a (7, 4) Hamming code. Each transmitted bit is received correctly with probability (1 $$-$$ $$\in$$), and flipped with probability $$\in$$. For each codeword transmission, the receiver performs minimum Hamming distance decoding, and correctly decodes the message bits if and only if the channel introduces at most one bit error. For $$\in$$ = 0.1, the probability that a transmitted codeword is decoded correctly is __________ (rounded off to two decimal places).
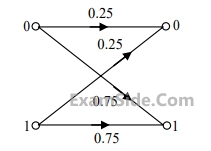The channel is$${x_0}$$ : a " zero " is transmitted
$${x_1}$$ : a " one " is transmitted
$${y_0}$$ : a " zero " is received
$${y_1}$$ : a " one " is received
The following probabilities are given:
$$P({x_0}) = \,{3 \over 4},\,\left( {\,\left. {{y_0}} \right|{x_0}} \right) = \,{1 \over 2},\,\,and\,P\,\,\left( {\,\left. {{y_0}} \right|{x_1}} \right) = \,{1 \over 2}$$.
The information in bits that you obtain when you learn which symbol has been received (while you know that a " zero " has been transmitted) is _____________
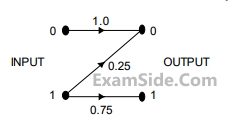If the output is 0, the probability that the input is also 0 equals____________________________________For a Fixed $${{P \over {{\sigma ^2}\,}} = 1000}$$, the channel capacity (in kbps) with infinite band width $$(W \to \infty )$$ is approximately
(a)lower___________.
(b) higher_________.